C++库Eigen学习3：稀疏线性代数

一条评论 / C/C++ / 作者： /

前情提要

C++库Eigen学习2：普通线性问题和分解

稀疏矩阵操作

头文件内容
#include <Eigen/SparseCore>稀疏矩阵、稀疏矢量、矩阵组装、基础稀疏线性代数
#include <Eigen/SparseCholesky>直接稀疏LLT、LDLT分解用于稀疏自伴随正定问题
#include<Eigen/SparseLU>稀疏LU分解用于一般二乘稀疏系统
#include<Eigen/SparseQR>稀疏QR分解用于稀疏线性最小二乘问题
#include <Eigen/IterativeLinearSolvers>迭代法求解大型一般线性二乘问题
#include <Eigen/Sparse>包含上面全部
所用到的库

稀疏矩阵格式

  • Values：各非零元素的值（column-major）
  • InnerIndices：各非零元素所在的行数
  • OuterStarts：每一列第一个出现的非零元素在前两个数组中的索引，末尾再添上前两个数组的长度
  • InnerNNZs：每列中非零元素的个数

例子如下

示例矩阵
无压缩模式下的各数组（有空闲空间“_”以插入新值）
压缩模式下的各数组

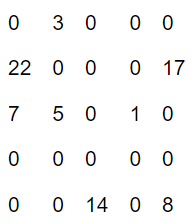
第一个例子（纯是没看懂）

使用有限差分法和Dirichlet边界条件在普通2D网格上求解拉普拉斯方程Δu=0

#include <Eigen/Sparse>
#include <vector>
#include <QImage>
 
typedef Eigen::SparseMatrix<double> SpMat; // declares a column-major sparse matrix type of double
typedef Eigen::Triplet<double> T;
 
void insertCoefficient(int id, int i, int j, double w, std::vector<T>& coeffs,
                       Eigen::VectorXd& b, const Eigen::VectorXd& boundary)
{
  int n = int(boundary.size());
  int id1 = i+j*n;
 
        if(i==-1 || i==n) b(id) -= w * boundary(j); // constrained coefficient
  else  if(j==-1 || j==n) b(id) -= w * boundary(i); // constrained coefficient
  else  coeffs.push_back(T(id,id1,w));              // unknown coefficient
}
 
void buildProblem(std::vector<T>& coefficients, Eigen::VectorXd& b, int n)
{
  b.setZero();
  Eigen::ArrayXd boundary = Eigen::ArrayXd::LinSpaced(n, 0,M_PI).sin().pow(2);
  for(int j=0; j<n; ++j)
  {
    for(int i=0; i<n; ++i)
    {
      int id = i+j*n;
      insertCoefficient(id, i-1,j, -1, coefficients, b, boundary);
      insertCoefficient(id, i+1,j, -1, coefficients, b, boundary);
      insertCoefficient(id, i,j-1, -1, coefficients, b, boundary);
      insertCoefficient(id, i,j+1, -1, coefficients, b, boundary);
      insertCoefficient(id, i,j,    4, coefficients, b, boundary);
    }
  }
}
 
void saveAsBitmap(const Eigen::VectorXd& x, int n, const char* filename)
{
  Eigen::Array<unsigned char,Eigen::Dynamic,Eigen::Dynamic> bits = (x*255).cast<unsigned char>();
  QImage img(bits.data(), n,n,QImage::Format_Indexed8);
  img.setColorCount(256);
  for(int i=0;i<256;i++) img.setColor(i,qRgb(i,i,i));
  img.save(filename);
}

稀疏矩阵类

SparseMatrix<std::complex<float> > mat(1000,2000);
// declares a 1000x2000 column-major compressed sparse matrix of complex<float>

SparseMatrix<double,RowMajor> mat(1000,2000);
// declares a 1000x2000 row-major compressed sparse matrix of double

SparseVector<std::complex<float> > vec(1000);
// declares a column sparse vector of complex<float> of size 1000

SparseVector<double,RowMajor> vec(1000);
// declares a row sparse vector of double of size 1000

获取矩阵信息

  • mat.rows()、mat.cols()、vec.size()
  • mat.innerSize()、mat.outerSize()
  • mat.nonZeros()、vec.nonZeros()

遍历非零元素：先遍历outer维度（每列），再遍历inter矢量（非零元素所在的列）

SparseMatrix<double> mat(rows,cols);
for (int k=0; k<mat.outerSize(); ++k)
  for (SparseMatrix<double>::InnerIterator it(mat,k); it; ++it)
  {
    it.value();
    it.row();   // row index
    it.col();   // col index (here it is equal to k)
    it.index(); // inner index, here it is equal to it.row()
  }
SparseVector<double> vec(size);
for (SparseVector<double>::InnerIterator it(vec); it; ++it)
{
  it.value(); // == vec[ it.index() ]
  it.index();
}

装填稀疏矩阵

typedef Eigen::Triplet<double> T;
std::vector<T> tripletList;
tripletList.reserve(estimation_of_entries);
for(...)
{
  // ...
  tripletList.push_back(T(i,j,v_ij)); // 猜测大概是行数、列数、值
}
SparseMatrixType mat(rows,cols);
mat.setFromTriplets(tripletList.begin(), tripletList.end());
// mat is ready to go!
SparseMatrix<double> mat(rows,cols);         // default is column major
mat.reserve(VectorXi::Constant(cols,6));     // 每列保留6个位置
for each i,j such that v_ij != 0
    mat.insert(i,j) = v_ij;                  // alternative: mat.coeffRef(i,j) += v_ij;
mat.makeCompressed();                        // optional

支持的运算符和函数

基础操作

加、减、取实部、取虚部、点积、转置、伴随

注意！存储方式必须相同，因此

SparseMatrix<double> A, B;
B = SparseMatrix<double>(A.transpose()) + A;

稀疏矩阵和普通矩阵可以混用

sm2 = sm1.cwiseProduct(dm1);
dm2 = sm1 + dm1;
dm2 = dm1 - sm1;
dm2 = dm1;
dm2 += sm1;
// 好于
dm2 = sm1 + dm1

矩阵乘积

稀疏-普通

dv2 = sm1 * dv1;
dm2 = dm1 * sm1.adjoint();
dm2 = 2. * sm1 * dm1;

对称稀疏-普通

dm2 = sm1.selfadjointView<>() * dm1;        // if all coefficients of A are stored
dm2 = A.selfadjointView<Upper>() * dm1;     // if only the upper part of A is stored
dm2 = A.selfadjointView<Lower>() * dm1;     // if only the lower part of A is stored

稀疏-稀疏

sm3 = sm1 * sm2;
sm3 = 4 * sm1.adjoint() * sm2;
sm3 = (sm1 * sm2).pruned();                  // removes numerical zeros
sm3 = (sm1 * sm2).pruned(ref);               // removes elements much smaller than ref
sm3 = (sm1 * sm2).pruned(ref,epsilon);       // removes elements smaller than ref*epsilon

置换矩阵

PermutationMatrix<Dynamic,Dynamic> P = ...;
sm2 = P * sm1;
sm2 = sm1 * P.inverse();
sm2 = sm1.transpose() * P;

分块操作

读的话和普通矩阵一样，写的话仅限于连续的列或行（存储方式为column-major或row-major的情况下）

SparseMatrix<double,ColMajor> sm1;
sm1.col(j) = ...;
sm1.leftCols(ncols) = ...;
sm1.middleCols(j,ncols) = ...;
sm1.rightCols(ncols) = ...;
 
SparseMatrix<double,RowMajor> sm2;
sm2.row(i) = ...;
sm2.topRows(nrows) = ...;
sm2.middleRows(i,nrows) = ...;
sm2.bottomRows(nrows) = ...;

三角化和自伴随（没懂）

三角化

dm2 = sm1.triangularView<Lower>(dm1);
dv2 = sm1.transpose().triangularView<Upper>(dv1);

自伴随

dm2 = sm1.selfadjointView<>() * dm1;        // if all coefficients of A are stored
dm2 = A.selfadjointView<Upper>() * dm1;     // if only the upper part of A is stored
dm2 = A.selfadjointView<Lower>() * dm1;     // if only the lower part of A is stored
sm2 = sm1.selfadjointView<Upper>();
// makes a full selfadjoint matrix from the upper triangular part
sm2.selfadjointView<Lower>() = sm1.selfadjointView<Upper>();
// copies the upper triangular part to the lower triangular part
PermutationMatrix<Dynamic,Dynamic> P = ...;
sm2 = A.selfadjointView<Upper>().twistedBy(P);
// compute P S P' from the upper triangular part of A, and make it a full matrix
sm2.selfadjointView<Lower>() = A.selfadjointView<Lower>().twistedBy(P);
// compute P S P' from the lower triangular part of A, and then only compute the lower part

求解稀疏线性系统

基本方法

#include <Eigen/RequiredModuleName>
// ...
SparseMatrix<double> A;
// fill A
VectorXd b, x;
// fill b
// solve Ax = b
SolverClassName<SparseMatrix<double> > solver;
solver.compute(A);
if(solver.info()!=Success) {
  // decomposition failed
  return;
}
x = solver.solve(b);
if(solver.info()!=Success) {
  // solving failed
  return;
}
// solve for another right hand side:
x1 = solver.solve(b1);

稀疏矩阵快速参考手册（重要）

https://eigen.tuxfamily.org/dox/group__SparseQuickRefPage.html

相关文章

1人评论了“C++库Eigen学习3：稀疏线性代数”

  1. Pingback: C++库Eigen学习4：几何 - Fivyex's Blog

发表评论

您的电子邮箱地址不会被公开。 必填项已用 * 标注

此站点使用Akismet来减少垃圾评论。了解我们如何处理您的评论数据。